

It is clear in the sequence above that the common difference f, is 2. The general form of an arithmetic sequence can be written as:
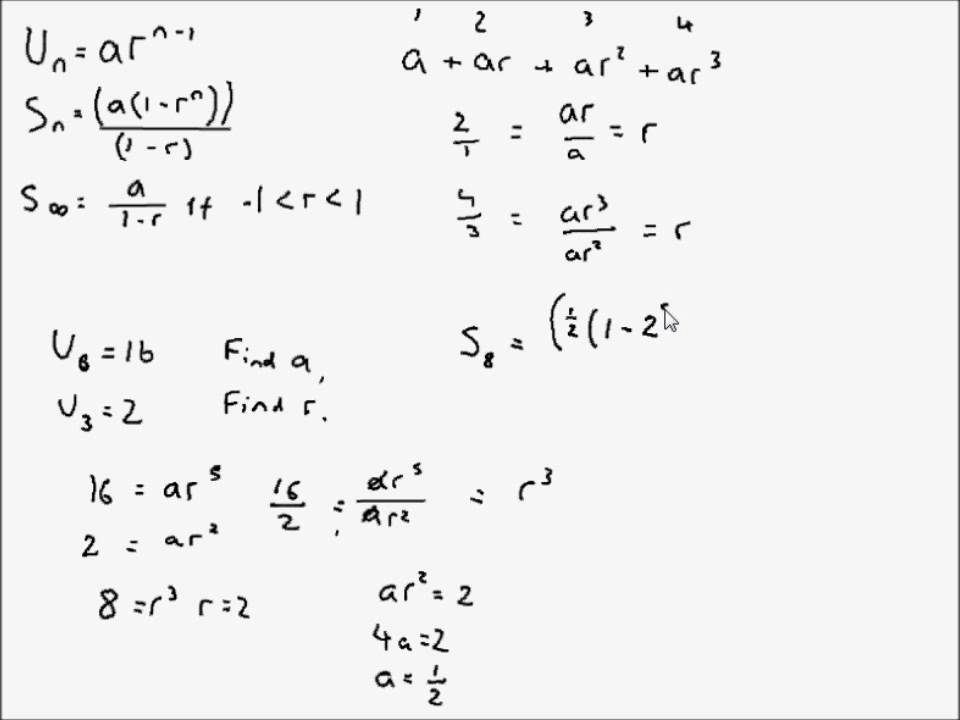
This difference can either be positive or negative, and dependent on the sign will result in terms of the arithmetic sequence tending towards positive or negative infinity. Arithmetic SequenceĪn arithmetic sequence is a number sequence in which the difference between each successive term remains constant. Indexing involves writing a general formula that allows the determination of the n th term of a sequence as a function of n. In cases that have more complex patterns, indexing is usually the preferred notation. There are multiple ways to denote sequences, one of which involves simply listing the sequence in cases where the pattern of the sequence is easily discernible.
Geometric and arithmetic sequences equations series#
They are particularly useful as a basis for series (essentially describe an operation of adding infinite quantities to a starting quantity), which are generally used in differential equations and the area of mathematics referred to as analysis. Sequences are used to study functions, spaces, and other mathematical structures. A series is convergent if the sequence converges to some limit, while a sequence that does not converge is divergent. Sequences have many applications in various mathematical disciplines due to their properties of convergence. There are many different types of number sequences, three of the most common of which include arithmetic sequences, geometric sequences, and Fibonacci sequences. In a number sequence, the order of the sequence is important, and depending on the sequence, it is possible for the same terms to appear multiple times. The individual elements in a sequence is often referred to as term, and the number of terms in a sequence is called its length, which can be infinite. Accordingly, a number sequence is an ordered list of numbers that follow a particular pattern. In mathematics, a sequence is an ordered list of objects. Where a is the first term in the sequence, r is the common ratio between the terms, and n is the number of terms in the sequence.Example: 1, 3, 5, 7, 9 11, 13.

To find the sum of a finite geometric sequence, use the following formula: For example, 1 + 3 + 9 + 27 + 81 = 121 is the sum of the first 5 terms of the geometric sequence. r -1 r > 1: sequence approaches positive infinity if a > 0 or negative infinity if a If r is negative, the sign of the terms in the sequence will alternate between positive and negative. If r is not -1, 1, or 0, the sequence will exhibit exponential growth or decay. Ī n = ar n-1 = 1(3 (12 - 1)) = 3 11 = 177,147ĭepending on the value of r, the behavior of a geometric sequence varies. Find the 12 th term of the geometric series: 1, 3, 9, 27, 81.


 0 kommentar(er)
0 kommentar(er)
